matrix_m Module
A matrix is a wrapper class for a rank 1 array of vector objects.
Matrices can be used to represent a variety of mathematical structures. This class is primarily used
to bind a selection of Linear Algebra algorithms to a matrix object. Matrices can be instantiated by assignment
of a rank2 array of any type, but the underlying data will be stored with double precision.
Matrix multiplication will be consistent with the mathematical operation (matmul), and element wise multiplication shall be represented by the hadamard product (OPERATOR .o.)
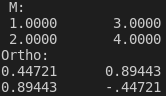
type(matrix) :: m, ortho_basis m = reshape([1, 2, 3, 4], [2, 2]) ! Create a 2x2 matrix print*, "M: " call m%print() ortho_basis = m%gram_schmidt() ! Compute an orthonormal basis using the Gram-Schmidt method print"(A)", "Ortho:" call ortho_basis%print()!!
output:
Uses
Interfaces
public interface matrix
Construct a matrix
-
private elemental function matrix_ctr_nk(n, k) result(A)
Create a new -by- matrix by passing the number of rows and the number of columns
Arguments
Type Intent Optional Attributes Name integer, intent(in) :: n The number of rows in
integer, intent(in) :: k The number of cols in
Return Value type(matrix)
-
private elemental function matrix_ctr_nk_int(n, k, val) result(A)
Create a new -by- matrix by passing the number of rows and the number of columns
Arguments
Type Intent Optional Attributes Name integer, intent(in) :: n The number of rows in
integer, intent(in) :: k The number of cols in
integer, intent(in) :: val Return Value type(matrix)
-
private elemental function matrix_ctr_nk_r32(n, k, val) result(A)
Create a new -by- matrix by passing the number of rows and the number of columns
Arguments
Type Intent Optional Attributes Name integer, intent(in) :: n The number of rows in
integer, intent(in) :: k The number of cols in
real(kind=real32), intent(in) :: val Return Value type(matrix)
-
private elemental function matrix_ctr_nk_r64(n, k, val) result(A)
Create a new -by- matrix by passing the number of rows and the number of columns
Arguments
Type Intent Optional Attributes Name integer, intent(in) :: n The number of rows in
integer, intent(in) :: k The number of cols in
real(kind=real64), intent(in) :: val Return Value type(matrix)
-
private pure function matrix_ctr_matrix(m2) result(A)
Create a new -by- matrix by passing a rank2 integer array
Arguments
Type Intent Optional Attributes Name class(matrix), intent(in) :: m2 Return Value type(matrix)
-
private pure function matrix_ctr_int(array) result(A)
Create a new -by- matrix by passing a rank2 integer array
Arguments
Type Intent Optional Attributes Name integer, intent(in), dimension(:,:) :: array Return Value type(matrix)
-
private pure function matrix_ctr_r32(array) result(A)
Create a new -by- matrix by passing a rank2 integer array
Arguments
Type Intent Optional Attributes Name real(kind=real32), intent(in), dimension(:,:) :: array Return Value type(matrix)
-
private pure function matrix_ctr_r64(array) result(A)
Create a new -by- matrix by passing a rank2 integer array
Arguments
Type Intent Optional Attributes Name real(kind=real64), intent(in), dimension(:,:) :: array Return Value type(matrix)
-
private pure function matrix_ctr_rank1_int(array, n, k) result(A)
Construct a -by- given a rank1 array of ints
Arguments
Type Intent Optional Attributes Name integer, intent(in), dimension(:) :: array integer, intent(in) :: n integer, intent(in) :: k Return Value type(matrix)
-
private pure function matrix_ctr_rank1_r32(array, n, k) result(A)
Construct a -by- given a rank1 array of ints
Arguments
Type Intent Optional Attributes Name real(kind=real32), intent(in), dimension(:) :: array integer, intent(in) :: n integer, intent(in) :: k Return Value type(matrix)
-
private pure function matrix_ctr_rank1_r64(array, n, k) result(A)
Construct a -by- given a rank1 array of ints
Arguments
Type Intent Optional Attributes Name real(kind=real64), intent(in), dimension(:) :: array integer, intent(in) :: n integer, intent(in) :: k Return Value type(matrix)
Derived Types
type, public :: matrix
Constructor
Construct a matrix
| private elemental function matrix_ctr_nk(n, k) | Create a new -by- matrix by passing the number of rows and the number of columns |
| private elemental function matrix_ctr_nk_int(n, k, val) | Create a new -by- matrix by passing the number of rows and the number of columns |
| private elemental function matrix_ctr_nk_r32(n, k, val) | Create a new -by- matrix by passing the number of rows and the number of columns |
| private elemental function matrix_ctr_nk_r64(n, k, val) | Create a new -by- matrix by passing the number of rows and the number of columns |
| private pure function matrix_ctr_matrix(m2) | Create a new -by- matrix by passing a rank2 integer array |
| private pure function matrix_ctr_int(array) | Create a new -by- matrix by passing a rank2 integer array |
| private pure function matrix_ctr_r32(array) | Create a new -by- matrix by passing a rank2 integer array |
| private pure function matrix_ctr_r64(array) | Create a new -by- matrix by passing a rank2 integer array |
| private pure function matrix_ctr_rank1_int(array, n, k) | Construct a -by- given a rank1 array of ints |
| private pure function matrix_ctr_rank1_r32(array, n, k) | Construct a -by- given a rank1 array of ints |
| private pure function matrix_ctr_rank1_r64(array, n, k) | Construct a -by- given a rank1 array of ints |
Type-Bound Procedures
| generic, public :: new => new_, new_matrix_ | Create a new matrix |
| procedure, public :: clear => clear_matrix | Clear all of the elements of a matrix |
| procedure, public :: print => print_matrix | Print the contents of a matrix |
| procedure, public :: vec => access_vector_matrix | Get the kth vector in the matrix |
| procedure, public :: at => at_index_matrix | Get the element at the index (i, j) |
| procedure, public :: gram_schmidt => gram_schmidt_matrix | Compute an otrthonormal basis for the vector space spanned by the columns of a matrix |
| procedure, public :: is_orthonormal => is_orthonormal_matrix | Check whether a matrix is orthonormal |
| procedure, public :: as_array => matrix_as_array | Return a rank2 Fortran array |
| procedure, public :: id => identity_matrix | |
| procedure, public :: ncol => matrix_ncol | Return the number of cols of A |
| procedure, public :: nrow => matrix_nrow | Return the number of rows of A |
| generic, public :: create_hh => create_hh_ | |
| generic, public :: fill => fill_int_, fill_r32_, fill_r64_ | |
| generic, public :: set => set_int_, set_r32_, set_r64_ | Set the value of (a_{i,j}) |
| generic, public :: assignment(=) => from_array_int_, from_array_r32_, from_array_r64_, from_matrix | Assign the contents of a matrix from a rank2 Fortran array |
| procedure, public :: get_row => matrix_get_row | |
| procedure, public :: get_col => matrix_get_col | |
| generic, public :: set_row => set_row_int_, set_row_r32_, set_row_r64_, set_row_vec_ | |
| generic, public :: set_col => set_col_int_, set_col_r32_, set_col_r64_, set_col_vec_ | |
| generic, public :: operator(+) => add_matrix_ | Operator interface to add two matrices |
| generic, public :: operator(-) => minus_matrix_ | Operator interface to subtract a matrix |
| generic, public :: operator(*) => times_matrix_, times_vector_ | Operator interface to multiply two matrices |
| generic, public :: operator(.o.) => hadamard_ | |
| generic, public :: operator(**) => to_the_n_ | |
| generic, public :: plus => add_matrix_sub_ | Subroutine interface to add two matrices |
| generic, public :: minus => minus_matrix_sub_ | Subroutine interface to add two matrices |
| generic, public :: times => times_int_sub_, times_r32_sub_, times_r64_sub_ |