module matrix_m !! A matrix is a wrapper class for a rank 1 array of vector objects. <br> !! Matrices can be used to represent a variety of mathematical structures. This class is primarily used !! to bind a selection of Linear Algebra algorithms to a matrix object. Matrices can be instantiated by assignment !! of a rank2 array of any type, but the underlying data will be stored with double precision. <br> !! !! Matrix multiplication will be consistent with the mathematical operation (matmul), and element wise multiplication !! shall be represented by the hadamard product (OPERATOR .o.) !! !!```fortran !!type(matrix) :: m, ortho_basis !! !!m = reshape([1, 2, 3, 4], [2, 2]) ! Create a 2x2 matrix !!print*, "M: " !!call m%print() !! !!ortho_basis = m%gram_schmidt() ! Compute an orthonormal basis using the Gram-Schmidt method !! !!print"(A)", "Ortho:" !!call ortho_basis%print()!! !!``` !! !!output: !! !!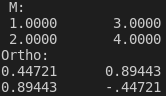 !! use vector_m use iso_fortran_env, only: real64, real32 implicit none private type, public :: matrix private integer :: k = 1 !! Number of vectors integer :: n = 1 !! Dimension of vectors type(vector), dimension(:), pointer :: m !! The vectors stored in a matrix logical :: m_allocated = .false. !! Allocation status of pointer contains private generic, public :: new => new_, new_matrix_ !! Create a new matrix procedure, public :: clear => clear_matrix !! Clear all of the elements of a matrix procedure, public :: print => print_matrix !! Print the contents of a matrix procedure, public :: vec => access_vector_matrix !! Get the kth vector in the matrix procedure, public :: at => at_index_matrix !! Get the element at the index (i, j) procedure, public :: gram_schmidt => gram_schmidt_matrix !! Compute an otrthonormal basis for the vector space spanned by the columns of a matrix procedure, public :: is_orthonormal => is_orthonormal_matrix !! Check whether a matrix is orthonormal procedure, public :: as_array => matrix_as_array !! Return a rank2 Fortran array procedure, public :: id => identity_matrix procedure, public :: ncol => matrix_ncol !! Return the number of cols of A procedure, public :: nrow => matrix_nrow !! Return the number of rows of A generic, public :: create_hh => create_hh_ procedure, nopass :: create_hh_ => matrix_create_householder_matrix generic, public :: fill => fill_int_, fill_r32_, fill_r64_ procedure :: fill_int_ => matrix_fill_int procedure :: fill_r32_ => matrix_fill_r32 procedure :: fill_r64_ => matrix_fill_r64 procedure :: conform_ => matrix_conform procedure :: mult_conform => matrix_mult_conform !! Check if two matrices are conforming for matrix multiplication (The number of cols of A should match the number of rows of B) generic, public :: set => set_int_, set_r32_, set_r64_ !! Set the value of \(a_{i,j}) generic, public :: assignment(=) => from_array_int_, from_array_r32_, from_array_r64_, from_matrix !! Assign the contents of a matrix from a rank2 Fortran array procedure :: new_ => new_matrix procedure :: new_matrix_ => new_matrix_from_matrix procedure, public :: get_row => matrix_get_row procedure, public :: get_col => matrix_get_col generic, public :: set_row => set_row_int_, set_row_r32_, set_row_r64_, set_row_vec_ generic, public :: set_col => set_col_int_, set_col_r32_, set_col_r64_, set_col_vec_ procedure :: set_row_int_ => matrix_set_row_array_int procedure :: set_row_r32_ => matrix_set_row_array_r32 procedure :: set_row_r64_ => matrix_set_row_array_r64 procedure :: set_row_vec_ => matrix_set_row_vec procedure :: set_col_int_ => matrix_set_col_array_int procedure :: set_col_r32_ => matrix_set_col_array_r32 procedure :: set_col_r64_ => matrix_set_col_array_r64 procedure :: set_col_vec_ => matrix_set_col_vec !=================Operator Functions===============! generic, public :: operator(+) => add_matrix_ !! Operator interface to add two matrices !!@Note !! As an operator, this procedure is a **function** which return a new matrix. !! use the functional operator equivalent, use [[]] generic, public :: operator(-) => minus_matrix_ !! Operator interface to subtract a matrix !!@Note !! As an operator, this procedure is a **function** which return a new matrix. !! use the functional operator equivalent, use [[]] generic, public :: operator(*) => times_matrix_, times_vector_ !! Operator interface to multiply two matrices !!@Note !! As an operator, this procedure is a **function** which return a new matrix. !! use the functional operator equivalent, use [[]] generic, public :: operator(.o.) => hadamard_ generic, public :: operator(**) => to_the_n_ !=================Operator Subroutines===============! generic, public :: plus => add_matrix_sub_ !! Subroutine interface to add two matrices !!@Note !! This subroutine will alter the passed matrix. To use the functional operator equivalent, use \(+\) ! generic, public :: times => times_matrix_sub_ generic, public :: minus => minus_matrix_sub_ !! Subroutine interface to add two matrices !!@Note !! This subroutine will alter the passed matrix. To use the functional operator equivalent, use \(+\) generic, public :: times => times_int_sub_, times_r32_sub_, times_r64_sub_ procedure :: hadamard_ => matrix_hadamard_matrix procedure :: to_the_n_ => matrix_to_the_n procedure :: add_matrix_ => matrix_add_matrix procedure :: add_matrix_sub_ => matrix_add_matrix_sub procedure :: minus_matrix_ => matrix_minus_matrix procedure :: minus_matrix_sub_ => matrix_minus_matrix_sub procedure :: times_matrix_ => matrix_times_matrix procedure :: times_int_sub_ => matrix_times_int_sub procedure :: times_r32_sub_ => matrix_times_r32_sub procedure :: times_r64_sub_ => matrix_times_r64_sub procedure :: times_vector_ => matrix_times_vector procedure :: from_array_int_ => matrix_from_rank2_array_int procedure :: from_array_r32_ => matrix_from_rank2_array_r32 procedure :: from_array_r64_ => matrix_from_rank2_array_r64 procedure :: from_matrix => matrix_from_matrix procedure :: set_int_ => set_index_matrix_int procedure :: set_r32_ => set_index_matrix_r32 procedure :: set_r64_ => set_index_matrix_r64 procedure :: alloc_ => allocate_matrix_data !! Allocate the space for an array containing the matrix's elements procedure :: dealloc_ => deallocate_matrix_data !! Deallocate the underlying container for a matrix's elements end type interface matrix !! Construct a matrix procedure :: matrix_ctr_nk procedure :: matrix_ctr_nk_int procedure :: matrix_ctr_nk_r32 procedure :: matrix_ctr_nk_r64 !! Construct a matrix by specifying its number of rows \(n\) and number of cols \(k\) procedure :: matrix_ctr_matrix procedure :: matrix_ctr_int procedure :: matrix_ctr_r32 procedure :: matrix_ctr_r64 procedure :: matrix_ctr_rank1_int procedure :: matrix_ctr_rank1_r32 procedure :: matrix_ctr_rank1_r64 end interface contains !=============================================================================! != Constructor Functions =! !=============================================================================! elemental subroutine new_matrix(self, n, k) !! Wipe the contents of a matrix and allocate the proper amount of space class(matrix), intent(inout) :: self !! Matrix object to wipe integer, intent(in) :: n !! Dimension of each constituent vector integer, intent(in) :: k !! Number of vectors call self%clear() if(k <= 0 .or. n <= 0) error stop "Cannot instantiate vector with 0 or negative dimension" self%k = k self%n = n call self%alloc_() end subroutine elemental function matrix_ctr_nk(n, k) result(A) !! Create a new \(n\)-by-\(k\) matrix \(A\) by passing the number of rows \(n\) and the number of columns \(k\) integer, intent(in) :: n !! The number of rows in \(m\) integer, intent(in) :: k !! The number of cols in \(m\) type(matrix) :: A call A%new_(n, k) call A%fill(0) end function elemental function matrix_ctr_nk_int(n, k, val) result(A) !! Create a new \(n\)-by-\(k\) matrix \(A\) by passing the number of rows \(n\) and the number of columns \(k\) integer, intent(in) :: n !! The number of rows in \(m\) integer, intent(in) :: k !! The number of cols in \(m\) integer, intent(in) :: val type(matrix) :: A call A%new_(n, k) call A%fill(val) end function elemental function matrix_ctr_nk_r32(n, k, val) result(A) !! Create a new \(n\)-by-\(k\) matrix \(A\) by passing the number of rows \(n\) and the number of columns \(k\) integer, intent(in) :: n !! The number of rows in \(m\) integer, intent(in) :: k !! The number of cols in \(m\) real(real32), intent(in) :: val type(matrix) :: A call A%new_(n, k) call A%fill(val) end function elemental function matrix_ctr_nk_r64(n, k, val) result(A) !! Create a new \(n\)-by-\(k\) matrix \(A\) by passing the number of rows \(n\) and the number of columns \(k\) integer, intent(in) :: n !! The number of rows in \(m\) integer, intent(in) :: k !! The number of cols in \(m\) real(real64), intent(in) :: val type(matrix) :: A call A%new_(n, k) call A%fill(val) end function pure function matrix_ctr_int(array) result(A) !! Create a new \(n\)-by-\(k\) matrix \(A\) by passing a rank2 integer array integer, dimension(:,:), intent(in) :: array type(matrix) :: A A = array end function pure function matrix_ctr_r32(array) result(A) !! Create a new \(n\)-by-\(k\) matrix \(A\) by passing a rank2 integer array real(real32), dimension(:,:), intent(in) :: array type(matrix) :: A A = array end function pure function matrix_ctr_r64(array) result(A) !! Create a new \(n\)-by-\(k\) matrix \(A\) by passing a rank2 integer array real(real64), dimension(:,:), intent(in) :: array type(matrix) :: A A = array end function pure function matrix_ctr_matrix(m2) result(A) !! Create a new \(n\)-by-\(k\) matrix \(A\) by passing a rank2 integer array class(matrix), intent(in) :: m2 type(matrix) :: A A = m2 end function pure function matrix_ctr_rank1_int(array, n, k) result(A) !! Construct a \(n\)-by-\(k\) given a rank1 array of ints integer, dimension(:), intent(in) :: array integer, intent(in) :: n integer, intent(in) :: k type(matrix) :: A if(size(array) /= (n * k)) error stop "Passed array and matrix size do not conform" A = reshape(array, [n, k]) end function pure function matrix_ctr_rank1_r32(array, n, k) result(A) !! Construct a \(n\)-by-\(k\) given a rank1 array of ints real(real32), dimension(:), intent(in) :: array integer, intent(in) :: n integer, intent(in) :: k type(matrix) :: A if(size(array) /= (n * k)) error stop "Passed array and matrix size do not conform" A = reshape(array, [n, k]) end function pure function matrix_ctr_rank1_r64(array, n, k) result(A) !! Construct a \(n\)-by-\(k\) given a rank1 array of ints real(real64), dimension(:), intent(in) :: array integer, intent(in) :: n integer, intent(in) :: k type(matrix) :: A if(size(array) /= (n * k)) error stop "Passed array and matrix size do not conform" A = reshape(array, [n, k]) end function elemental subroutine new_matrix_from_matrix(self, m2) !! Wipe the contents of a matrix and allocate the proper amount of space class(matrix), intent(inout) :: self !! Matrix object to wipe class(matrix), intent(in) :: m2 !! Matrix object to wipe call self%clear() self%k = m2%k self%n = m2%n call self%alloc_() end subroutine pure subroutine matrix_from_rank2_array_int(self, array) !! Assign a matrix from a rank2 integer array class(matrix), intent(inout) :: self integer, dimension(:,:), intent(in) :: array integer :: i, k, n n = size(array, dim=1) k = size(array, dim=2) call self%new(n, k) do i = 1, k self%m(i) = array(:,i) end do end subroutine pure subroutine matrix_from_rank2_array_r32(self, array) !! Assign a matrix from a rank2 single precision real array class(matrix), intent(inout) :: self real(real32), dimension(:,:), intent(in) :: array integer :: i, k, n n = size(array, dim=1) k = size(array, dim=2) call self%new(n, k) do i = 1, k self%m(i) = array(:,i) end do end subroutine pure subroutine matrix_from_rank2_array_r64(self, array) !! Assign a matrix from a rank2 double precision array class(matrix), intent(inout) :: self real(real64), dimension(:,:), intent(in) :: array integer :: i, k, n n = size(array, dim=1) k = size(array, dim=2) call self%new(n, k) do i = 1, k self%m(i) = array(:,i) end do end subroutine elemental subroutine matrix_from_matrix(self, m) !! class(matrix), intent(inout) :: self class(matrix), intent(in) :: m integer :: i self%n = m%n self%k = m%k call self%new(m%n, m%k) do i = 1, self%k self%m(i) = m%vec(i) end do end subroutine elemental subroutine matrix_from_val_int(self, val) class(matrix), intent(inout) :: self integer, intent(in) :: val if(self%m_allocated) then call self%fill(val) else self = matrix(1,1,val) end if end subroutine elemental subroutine matrix_from_val_r32(self, val) class(matrix), intent(inout) :: self real(real32), intent(in) :: val if(self%m_allocated) then call self%fill(val) else self = matrix(1,1,val) end if end subroutine elemental subroutine matrix_from_val_r64(self, val) class(matrix), intent(inout) :: self real(real64), intent(in) :: val if(self%m_allocated) then call self%fill(val) else self = matrix(1,1,val) end if end subroutine elemental subroutine matrix_fill_int(self, val) ! Fill the matrix, don't ask any questions class(matrix), intent(inout) :: self integer, intent(in) :: val integer :: i do i = 1, self%k self%m(i) = val end do end subroutine elemental subroutine matrix_fill_r32(self, val) ! Fill the matrix, don't ask any questions class(matrix), intent(inout) :: self real(real32), intent(in) :: val integer :: i do i = 1, self%k self%m(i) = val end do end subroutine elemental subroutine matrix_fill_r64(self, val) ! Fill the matrix, don't ask any questions class(matrix), intent(inout) :: self real(real64), intent(in) :: val integer :: i do i = 1, self%k self%m(i) = val end do end subroutine elemental subroutine clear_matrix(self) class(matrix), intent(inout) :: self self%k = 0 self%n = 0 if (self%m_allocated) then call self%dealloc_() end if end subroutine elemental subroutine allocate_matrix_data(self) class(matrix), intent(inout) :: self integer :: ierr allocate(self%m(self%k), STAT=ierr) call self%m%set_zero(self%n) if (ierr /= 0) error stop "Error allocating vector" self%m_allocated = .true. end subroutine elemental subroutine deallocate_matrix_data(self) class(matrix), intent(inout) :: self integer :: ierr call self%m%dealloc_() deallocate(self%m, STAT=ierr) if (ierr /= 0) error stop "Error allocating vector" self%m_allocated = .false. end subroutine subroutine print_matrix(self) class(matrix), intent(in) :: self character(10) :: num_fmt character(100) :: fmt integer :: i, j write(num_fmt,"(I0)") self%k fmt = "(" // num_fmt // "(G11.5, 2X))" ! fmt = "(" // num_fmt // "(G0, 2X))" do i = 1, self%n print fmt, (self%at(i, j), j = 1, self%k) end do end subroutine !=============================================================================! != Inquiry Functions =! !=============================================================================! elemental function at_index_matrix(self, i, j) result(element) class(matrix), intent(in) :: self integer, intent(in) :: i !! ith element integer, intent(in) :: j !! jth vector real(real64) :: element element = self%m(j)%at(i) end function elemental subroutine set_index_matrix_int(self, i, j, x) class(matrix), intent(inout) :: self integer, intent(in) :: i !! ith element integer, intent(in) :: j !! jth vector integer, intent(in) :: x call self%m(j)%set(i, x) end subroutine elemental subroutine set_index_matrix_r32(self, i, j, x) class(matrix), intent(inout) :: self integer, intent(in) :: i !! ith element integer, intent(in) :: j !! jth vector real(real32), intent(in) :: x call self%m(j)%set(i, x) end subroutine elemental subroutine set_index_matrix_r64(self, i, j, x) class(matrix), intent(inout) :: self integer, intent(in) :: i !! ith element integer, intent(in) :: j !! jth vector real(real64), intent(in) :: x call self%m(j)%set(i, x) end subroutine elemental function access_vector_matrix(self, v) result(vec) !! Get a copy of the vth vector class(matrix), intent(in) :: self integer, intent(in) :: v type(vector) :: vec if (v < 1 .or. v > self%k) error stop "Out of bounds index" vec = self%m(v) end function elemental function matrix_get_row(self, i) result(row_i) class(matrix), intent(in) :: self integer, intent(in) :: i !! \(i\)th row type(vector) :: row_i integer :: irow row_i = vector(self%k) ! Create vector with dimension = number of self's cols do irow = 1,self%k call row_i%set(irow, self%at(i,irow)) end do end function elemental function matrix_get_col(self, j) result(col_j) class(matrix), intent(in) :: self integer, intent(in) :: j !! \(j\)th row type(vector) :: col_j col_j = self%m(j) end function elemental subroutine matrix_set_col_vec(self, j, vec) class(matrix), intent(inout) :: self integer, intent(in) :: j !! Column number class(vector), intent(in) :: vec self%m(j) = vec end subroutine pure subroutine matrix_set_col_array_int(self, j, array) class(matrix), intent(inout) :: self integer, intent(in) :: j !! Column number integer, dimension(:), intent(in) :: array if(size(array) /= self%n) error stop "Length of passed array not compatible with matrix n" self%m(j) = array end subroutine pure subroutine matrix_set_col_array_r32(self, j, array) class(matrix), intent(inout) :: self integer, intent(in) :: j !! Column number real(real32), dimension(:), intent(in) :: array if(size(array) /= self%n) error stop "Length of passed array not compatible with matrix n" self%m(j) = array end subroutine pure subroutine matrix_set_col_array_r64(self, j, array) class(matrix), intent(inout) :: self integer, intent(in) :: j !! Column number real(real64), dimension(:), intent(in) :: array if(size(array) /= self%n) error stop "Length of passed array not compatible with matrix n" self%m(j) = array end subroutine elemental subroutine matrix_set_row_vec(self, i, vec) class(matrix), intent(inout) :: self integer, intent(in) :: i !! Row number class(vector), intent(in) :: vec integer :: icol if(vec%size() /= self%k) error stop "Length of passed array not compatible with matrix k" do icol = 1, self%k call self%set(i, icol, vec%at(icol)) end do end subroutine pure subroutine matrix_set_row_array_int(self, i, array) class(matrix), intent(inout) :: self integer, intent(in) :: i !! Row number integer, dimension(:), intent(in) :: array integer :: icol if(size(array) /= self%k) error stop "Length of passed array not compatible with matrix k" do icol = 1, self%k call self%set(i, icol, array(icol)) end do end subroutine pure subroutine matrix_set_row_array_r32(self, i, array) class(matrix), intent(inout) :: self integer, intent(in) :: i !! Row number real(real32), dimension(:), intent(in) :: array integer :: icol if(size(array) /= self%k) error stop "Length of passed array not compatible with matrix k" do icol = 1, self%k call self%set(i, icol, array(icol)) end do end subroutine pure subroutine matrix_set_row_array_r64(self, i, array) class(matrix), intent(inout) :: self integer, intent(in) :: i !! Row number real(real64), dimension(:), intent(in) :: array integer :: icol if(size(array) /= self%k) error stop "Length of passed array not compatible with matrix k" do icol = 1, self%k call self%set(i, icol, array(icol)) end do end subroutine elemental function gram_schmidt_matrix(self) result(ortho) class(matrix), intent(in) :: self type(matrix) :: ortho integer i, j, n, k n = self%n k = self%k if(k > n) k = n !! If there are more vectors than the dimension of the vector, only output n vectors call ortho%new(n, k) ! print *, "dimension of input basis = ", self%n ! print *, "number of basis vectors = ", self%k ! print *, "orthonormal_basis set to 0" ortho%m(1) = self%m(1)%normalized() do i = 2,k ortho%m(i) = self%m(i) do j = 1,i-1 ortho%m(i) = ortho%m(i) - (ortho%m(i) .proj. ortho%m(j)) ! ortho%m(i) = (ortho%m(i) .proj. ortho%m(j)) - ortho%m(i) end do call ortho%m(i)%normalize() end do end function elemental function is_orthonormal_matrix(self) result(bool) class(matrix), intent(in) :: self logical :: bool integer :: i, j if(all(self%m%is_normal())) then do i = 1,self%k do j = i+1,self%k if (.not. self%m(i)%is_ortho(self%m(j))) then bool = .false. return end if end do end do bool = .true. else bool = .false. end if end function pure function matrix_as_array(self) result(array) class(matrix), intent(in) :: self real(real64), dimension(self%n, self%k) :: array integer :: j do j = 1, self%k array(:,j) = self%m(j)%data() end do end function elemental function matrix_conform(self, m2) result(bool) !! Check if two matrices are conforming (have the same dimensions) class(matrix), intent(in) :: self class(matrix), intent(in) :: m2 logical :: bool !! True when self%dim == v2%dim bool = (self%k == m2%k .and. self%n == m2%n) end function elemental function matrix_mult_conform(self, m2) result(bool) !! Check if two matrices are conforming (have the same dimensions) class(matrix), intent(in) :: self class(matrix), intent(in) :: m2 logical :: bool !! True when self%k == v2%n bool = (self%k == m2%n) end function !=============================================================================! != Function Operators =! !=============================================================================! elemental function matrix_add_matrix(self, m2) result(m3) class(matrix), intent(in) :: self class(matrix), intent(in) :: m2 type(matrix) :: m3 if(.not. self%conform_(m2)) error stop "Cannot add nonconforming matrices" m3 = self call m3%m%plus(m2%m) end function elemental function matrix_minus_matrix(self, m2) result(m3) class(matrix), intent(in) :: self class(matrix), intent(in) :: m2 type(matrix) :: m3 if(.not. self%conform_(m2)) error stop "Cannot add nonconforming matrices" m3 = self call m3%m%minus(m2%m) end function elemental function matrix_times_matrix(self, m2) result(m3) class(matrix), intent(in) :: self class(matrix), intent(in) :: m2 type(matrix) :: m3 integer :: i, j if(.not. self%conform_(m2)) error stop "Cannot add nonconforming matrices" m3 = matrix(self%n, m2%k) do i = 1, m3%n do j = 1, m3%k call m3%set(i,j, (self%get_row(i) .dot. m2%get_col(j))) ! The i,j element is equal to the ith row of self times the jth column of m2 end do end do end function elemental function matrix_times_vector(self, v) result(v2) class(matrix), intent(in) :: self class(vector), intent(in) :: v type(vector) :: v2 integer :: i if(self%k /= v%size()) error stop "Cannot add nonconforming matrices" v2 = vector(self%n) do i = 1, self%n call v2%set(i, self%get_row(i) .dot. v) end do end function elemental function matrix_hadamard_matrix(self, m2) result(m3) class(matrix), intent(in) :: self class(matrix), intent(in) :: m2 type(matrix) :: m3 if(.not. self%conform_(m2)) error stop "Cannot multiply two nonconforming matrices" m3 = self call m3%m%times(m2%m) ! Use elemental function call to multiply all the columns by eachother!!! end function elemental function matrix_to_the_n(self, n) result(m2) !! Raise a matrix to the nth power. Must be a square matrix class(matrix), intent(in) :: self integer, intent(in) :: n type(matrix) :: m2 integer :: i if(self%k /= self%n) error stop "Cannot raise non-square matrix to the nth power" if(n == 0) then m2 = m2%id(self%k) return else if(n == 1) then m2 = self return else if (n < 1) then error stop "Cannot raise matrix to a negative power" end if m2 = self do i = 1, n m2 = self * m2 end do end function !=============================================================================! != Subroutine Operators =! !=============================================================================! elemental subroutine matrix_add_matrix_sub(self, m2) !! Subroutine interface to add two matrices !!@Note !! This subroutine will alter the passed matrix. To use the functional operator equivalent, use \(+\) class(matrix), intent(inout) :: self class(matrix), intent(in) :: m2 if(.not. self%conform_(m2)) error stop "Cannot add nonconforming matrices" call self%m%plus(m2%m) end subroutine elemental subroutine matrix_minus_matrix_sub(self, m2) class(matrix), intent(inout) :: self class(matrix), intent(in) :: m2 if(.not. self%conform_(m2)) error stop "Cannot add nonconforming matrices" call self%m%minus(m2%m) end subroutine elemental subroutine matrix_times_int_sub(self, val) class(matrix), intent(inout) :: self integer, intent(in) :: val call self%m%times(val) end subroutine elemental subroutine matrix_times_r32_sub(self, val) class(matrix), intent(inout) :: self real(real32), intent(in) :: val call self%m%times(val) end subroutine elemental subroutine matrix_times_r64_sub(self, val) class(matrix), intent(inout) :: self real(real64), intent(in) :: val call self%m%times(val) end subroutine elemental function identity_matrix(self, n) result(I_n) !! Return \(I_n\) class(matrix), intent(in) :: self integer, optional, value :: n type(matrix) :: I_n integer :: n_, i if(present(n)) then n_ = n else n_ = self%n end if I_n = matrix(n_, n_) do i = 1, n_ call I_n%set(i,i,1) end do end function elemental function matrix_create_householder_matrix(normal) result(m) class(vector), intent(in) :: normal !! A UNIT vector that is normal to a plane of rotation type(matrix) :: m, op m = m%id(normal%size()) op = normal .outer. normal call op%times(2) call m%minus(op) end function elemental function matrix_ncol(self) result(icol) class(matrix), intent(in) :: self integer :: icol icol = self%k end function elemental function matrix_nrow(self) result(irow) class(matrix), intent(in) :: self integer :: irow irow = self%n end function ! elemental function matrix_create_krylov(self) result(K) ! end function end module